Египетский треугольник | Любопытные подробности обо всем на свете!
Название «египетский треугольник» появилось уже в 5 веке до н.э. Принадлежит оно прямоугольному треугольнику, стороны которого равны соответственно 3, 4 и 5.
Назван он был так потому, что очень широко применялся еще в Древнем Египте в различных сферах жизнедеятельности.
Хотя уже тогда он был знаком людям далеко за пределами Древнего Египта, но, видимо, его уникальные свойства заметили и начали использовать впервые именно там.
В чем же состоит его отличительная особенность?
Во-первых, все его стороны и площадь — это целые числа;
во-вторых, сумма квадратов катетов равна квадрату гипотенузе ( а это ведь теорема Пифагора, которую все знают со школы! Но о Пифагоре чуть позже);
в-третьих, это то, что с его помощью можно отмерять прямые углы в пространстве (треугольник-то прямоугольный!), а это просто необходимо, например, в строительстве;
и, в-четвертых, этот треугольник можно запросто построить с помощью простой веревки.
В пространстве достаточно сложно отложить прямой угол, (как же это сделать, когда в природе редко встретишь прямые линии, а уж тем более прямые углы, не от чего отталкиваться!), но египтяне изобрели интересный способ. Они брали веревку, отмеряли на ней узелками 12 частей, а потом складывали из нее треугольник, стороны которого равны 3 , 4 и 5 частям соответственно. В этом треугольнике прямой угол получался сам собой! А уже имея такой инструмент, они могли с большой точностью строить свои сооружения, например, пирамиды. А также использовать его для разметки земли под сельскохозяйственные работы.
А теперь про Пифагора. Египетский треугольник тесно связан с его именем.
Возможно, изучение интересных особенностей египетского треугольника и подтолкнуло Пифагора на попытку обобщения зависимостей во всех других прямоугольных треугольниках. Что ему, как известно, удалось!
Кстати, оказывается, теорема Пифагора попала в Книгу Рекордов Гиннеса как теорема с самым большим количеством доказательств (их насчитывается около 500).
История
Знаменитый греческий математик и философ Пифагор Самосский, давший свое имя теореме, жил 2,5 тыс. лет назад. Биография этого выдающегося ученого мало изучена, однако до сегодняшнего времени все же дошли некоторые .
По просьбе Фалеса, с целью изучения математики и астрономии, в 535 году до нашей эры он отправился в длинное путешествие в Египет и Вавилон. В Египте среди бескрайнего простора пустыни он увидел величественные пирамиды, изумляющие своими огромными размерами и стройными геометрическими формами. Стоит отметить, что Пифагор их лицезрел в несколько ином виде, чем тот, в котором видят туристы сейчас. Это были невообразимо огромные для того времени сооружения с четкими ровными гранями на фоне прилегающих храмов поменьше, для жен, детей и других родственников фараона. Кроме прямого назначения (усыпальницы и хранителя священного тела фараона) пирамиды сооружались и как символы величия, богатства и могущества Египта.
И вот Пифагор в ходе тщательного изучения этих конструкций заметил строгую закономерность в соотношении размеров и форм сооружений. Размерам Египетского треугольника соответствует пирамида Хеопса, она считалась священной и носила особенный магический смысл.
Египетский треугольник в строительстве. Общие сведения
Зарождение идеи
Идея у математика появилась после путешествия в Африку по просьбе Фалеса, который поставил задачу Пифагору изучить математику и астрономию тех мест. В Египте он среди бескрайней пустыни встретил величественные строения, поразившие его размером, изяществом и красотой.
Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.
Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.
Из истории
Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.
Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.
Строение
Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.
Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.
Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?
Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.
Обратное доказательство
Как доказать, что треугольник прямоугольный? Нужно порой исходить от обратного, то есть если сумма квадратов обеих сторон равна квадрату третьей, то треугольник прямоугольный, что подтверждает равенство 32х42=52 и значит он действительно прямоугольный.
Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».
Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.
Особенности
Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:
- все стороны и площадь состоят из целых чисел, как говорилось выше;
- согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
- такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
- не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.
Применение египетского треугольника
В Древние века в архитектуре и строительстве египетский треугольник пользовался огромной популярностью. Особенно он был необходим, если для построения прямого угла использовали веревку или шнур.
Ведь известно, что отложить прямой угол в пространстве, является довольно таки сложным занятием и поэтому предприимчивые египтяне изобрели интересный способ построения прямого угла. Для этих целей они брали веревку, на которой отмечали узелками двенадцать ровных частей и потом с этой веревки складывали треугольник, со сторонами, которые равнялись 3 , 4 и 5 частям и в итоге без проблем, получали прямоугольный треугольник. Благодаря такому замысловатому инструменту, египтяне с огромной точностью размеряли землю для сельскохозяйственных работ, строили дома и пирамиды.
Вот так посещение Египта и изучение особенностей египетской пирамиды подтолкнуло Пифагора на открытие своей теоремы, которая, кстати, попала в Книгу Рекордов Гиннеса, как теорема, которая имеет самое большое количество доказательств.
Треугольные колеса Рело
Колесо— круглый (как правило), свободно вращающийся или закреплённый на оси диск, позволяющий поставленному на него телу катиться, а не скользить. Колесо повсеместно используется в различных механизмах и инструментах. Широко применяется для транспортировки грузов.
Колесо существенно уменьшает затраты энергии на перемещение груза по относительно ровной поверхности. При использовании колеса работа совершается против силы трения качения, которая в искусственных условиях дорог существенно меньше, чем сила трения скольжения. Колёса бывают сплошные (например, колёсная пара железнодорожного вагона) и состоящие из довольно большого количества деталей, к примеру, в состав автомобильного колеса входит диск, обод, покрышка, иногда камера, болты крепления и тд. Износ покрышек автомобилей является почти решённой проблемой (при правильно установленных углах колёс). Современные покрышки проезжают свыше 100 000 км. Нерешённой проблемой является износ покрышек у колёс самолётов. При соприкосновении неподвижного колеса с бетонным покрытием взлётной полосы на скорости в несколько сотен километров в час износ покрышек огромен.
- В июле 2001 года на колесо был получен инновационный патент со следующей формулировкой: «круглое устройство, применяемое для транспортировки грузов». Этот патент был выдан Джону Кэо, юристу из Мельбурна, который хотел тем самым показать несовершенство австралийского патентного закона .
- Французская компания Мишлен в 2009 году разработала пригодное к массовому выпуску автомобильное колесо Active Wheel со встроенными электродвигателями, приводящими в действие колесо, рессору, амортизатор и тормоз. Таким образом, эти колёса делают ненужными следующие системы автомобиля: двигатель, сцепление, коробку передач, дифференциал, приводной и карданный валы.
- В 1959 году американец А. Сфредд получил патент на квадратное колесо. Оно легко шло по снегу, песку, грязи, преодолевало ямы. Вопреки опасениям, машина на таких колёсах не «хромала» и развивала скорость до 60 км/ч.
Франц Рело (Franz Reuleaux, 30 сентября 1829 — 20 августа 1905) — немецкий инженер-механик, лектор Берлинской Королевской Технической академии, ставший впоследствии ее президентом. Первым, в 1875 году, разработал и изложил основные положения структуры и кинематики механизмов; занимался проблемами эстетичности технических объектов, промышленным дизайном, в своих конструкциях придавал большое значение внешним формам машин. Рело часто называют отцом кинематики.
Мифы и легенды
История с обрушением подвесного Египетского моста в воду спровоцировала рост многих мистический версий объяснения. Существуют даже городские легенды об этом событии. Так, по одной из них, между молодой жительницей Санкт-Петербурга, проживающей неподалеку от моста, и военным офицером был роман.
Но офицер повел себя непорядочно, обманул девушку. И тогда она обозлилась. Однажды, увидев проезжающий по мосту полк из окна своего дома, она громко крикнула «Чтоб вам всем провалиться на месте!», что сразу же и произошло.
Многие также обвиняют в аварии сфинксов. Скульптуры были сделаны на месте. Они никогда не имели никакой связи с Древним Египтом, но простые люди одаривали их самыми различными сверхъестественными способностями. Люди считали, что мост не просто «поет» из-за скрипящих цепей, а поют сами сфинксы, причем исключительно погребальные песни.
Египетский треугольник в строительстве
Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.
Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника. Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
Стороны конструкции имеют следующее соотношение друг к другу:
Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:
- 5,
- 4,
Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.
Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов. Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять
В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять
Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.
Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.
Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам
Альтернативные способы построить прямой угол на 90 градусов
Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.
Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.
Как получить египетский треугольник при помощи верёвки
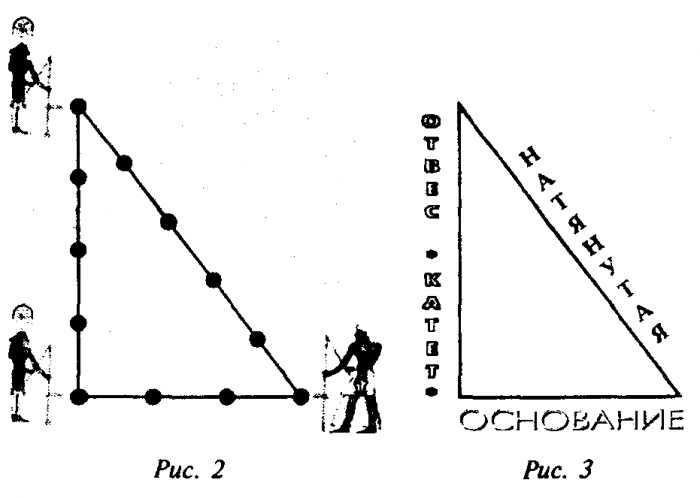
Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.
Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.
Как построить угол в 45, 30 и 60 градусов
Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.
Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть
Края должны совпасть.
Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.
Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках
Начинаем разметку от первой стены
Первым делом проверим нашу первую стену на вертикаль и плоскость. Если выравниваем 2 угла, то это стена, параллельная ванне, если выравниваем 4 угла (всю площадь), то стена с проёмом. Если стена завалена, её нужно будет выровнять первым делом, но не торопитесь, ведь мы ещё не проверили всю площадь.
Для начала просто отобьём ровную линию параллельно первой стене, максимально приближённую к ней.
Проведём первую линию, параллельно первой стены
Далее между первой стеной и второй стеной установим угольник одной гранью параллельно первой линии, а на вторую грань угольника накладываем прави́ло. Совмещаем грань прави́ла и угольника, тем самым «удлинняя» наш угольник. Чертим линию на полу до конца стены максимально приближённую к стене. Регулируем и совмещаем наш увеличенный угольник так что бы:
- линия была ровной,
- расстояние до стены минимальным,
- вторая грань угольника была параллельна первой линии.
Так получаем первый прямой угол.
От первой линии отобьём вторую, перпендикулярную ей
Далее идём на следующий угол, до которого мы чертили линию, и совмещаем угольник одной гранью параллельно второй линии. Повторяем процедуру с правилом (совмещаем его с угольником) и чертим третью линию перпендикулярную второй, опять же максимально приближённую к стене.
Тут требуется некоторая сноровка, чтобы совмещать прави́ло, угольник и делать прямой угол с линиями, максимально приближёнными к стене (это делается для того, что бы при штукатурке «не съесть» лишнее пространство). Если прави́ла не хватает, дочерчиваем до куда хватает, переставляем прави́ло, совмещая его с линией, и проводим её до конца стены.
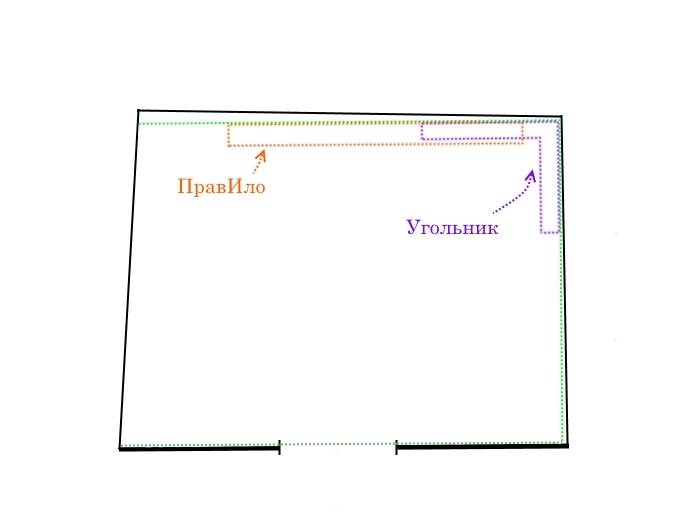
Чертим третью линию перпендикулярную второй
Чертим четвёртую линию, по аналогии. В итоге у нас должен получится начерченный на полу прямоугольник внутри нашего помещения. Проверяем его по первой грани — по стене с проёмом, так же, прикладывая угольник и правило.
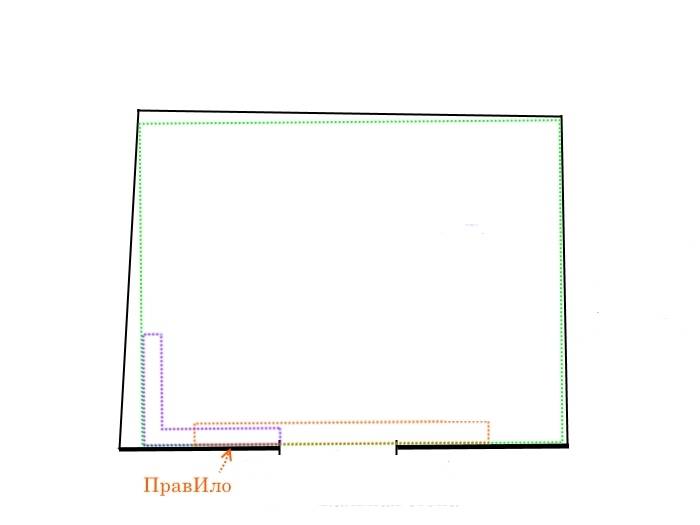
Проверяем по 1-й грани полученный прямоугольник
Если всё ровно, можно немного расслабиться. Если нет, повторяем процедуру и/или смотрим где ошиблись.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером
в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены —
это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250
см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат
(умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 —
это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра
должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали —
проверяемый угол развернут и имеет отклонение от 90°.
Калькулятор расчета диагонали прямого угла
Длина a
Длина b Расчет
Диагональ c
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены
на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.
Почти равносторонние треугольники Герона
Поскольку площадь равностороннего треугольника с рациональными сторонами является иррациональным числом , ни один равносторонний треугольник не является героновым. Однако существует уникальная последовательность треугольников Герона, которые являются «почти равносторонними», поскольку три стороны имеют форму n — 1, n , n + 1. Метод генерации всех решений этой задачи на основе цепных дробей описан в 1864 г. Эдвард Санг , а в 1880 г. Рейнхольд Хоппе дал замкнутое выражение для решений. Первые несколько примеров этих почти равносторонних треугольников перечислены в следующей таблице (последовательность A003500 в OEIS ):
| Длина стороны | Площадь | Inradius | ||
|---|---|---|---|---|
| п — 1 | п | п + 1 | ||
| 3 | 4 | 5 | 6 | 1 |
| 13 | 14 | 15 | 84 | 4 |
| 51 | 52 | 53 | 1170 | 15 |
| 193 | 194 | 195 | 16296 | 56 |
| 723 | 724 | 725 | 226974 | 209 |
| 2701 | 2702 | 2703 | 3161340 | 780 |
| 10083 | 10084 | 10085 | 44031786 | 2911 |
| 37633 | 37634 | 37635 | 613283664 | 10864 |
Последующие значения n можно найти, умножив предыдущее значение на 4, а затем вычтя предыдущее значение (52 = 4 × 14 — 4, 194 = 4 × 52 — 14 и т. Д.), Таким образом:
- птзнак равно4пт-1-пт-2,{\ Displaystyle п_ {т} = 4n_ {т-1} -n_ {т-2} \ ,,}
где t обозначает любую строку в таблице. Это последовательность Лукаса . В качестве альтернативы формула генерирует все n . Аналогично, пусть A = площадь и y = радиус, тогда
(2+3)т+(2-3)т{\ displaystyle (2 + {\ sqrt {3}}) ^ {t} + (2 — {\ sqrt {3}}) ^ {t}}
- ((п-1)2+п2+(п+1)2)2-2((п-1)4+п4+(п+1)4)знак равно(6пу)2знак равно(4А)2{\ displaystyle {\ big (} (n-1) ^ {2} + n ^ {2} + (n + 1) ^ {2} {\ big)} ^ {2} -2 {\ big (} ( n-1) ^ {4} + n ^ {4} + (n + 1) ^ {4} {\ big)} = (6ny) ^ {2} = (4A) ^ {2}}
где { n , y } — решения n 2 — 12 y 2 = 4. Небольшое преобразование n = 2x дает обычное уравнение Пелла x 2 — 3 y 2 = 1, решения которого затем могут быть получены из регулярного продолжения дробное разложение для √ 3 .
Переменная n имеет вид , где k равно 7, 97, 1351, 18817,…. Числа в этой последовательности обладают тем свойством, что k последовательных целых чисел имеют целое стандартное отклонение .
пзнак равно2+2k{\ displaystyle n = {\ sqrt {2 + 2k}}}
Небольшие хитрости
Египетский треугольник 3х4х5 актуален для маленьких домов. Но, что делать, если дом 12х15?
Для этого нужно построить прямоугольный треугольник, у которого катеты равняются 12 и 15 м. Гипотенуза находится как квадратный корень из суммы 12х12 и 15х15. В итоге получаем 19,2 м. С помощью чего-либо — веревки, шпагата, бечевки, тросика, военного кабеля, отмеряем 12, 15 и 19,2 м. Делаем узлы на этих местах и ставим жимки.
Затем треугольник нужно растянуть на нужном месте и установить 3 точки опоры, в которые вбить колышки. Четвертую точку можно получить, не трогая концы катетов. Для этого точка прямого угла перекидывается по диагонали и все готово.
Например, есть участок, где требуется прямой угол – для места под кухонный гарнитур, раскладки кафеля и других моментов. Хорошо бы такие вопросы учесть при кладке, но реальность другая и не всегда попадаются ровные стены и прямые углы. Здесь пригодится египетский треугольник с соотношением 3:4:5, либо при необходимости 1,5:2:2,5.
Обязательно учитывается толщина маяков, погрешность, бугры на стенах и т.д. Треугольник рисуется с помощью рулетки и мела. Если разметка небольшая, то можно воспользоваться листом гипсокартона, так как режутся они с правильными углами.
Египетский треугольник широко использовался в строительстве целых 2,5 века. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись. С ним легко работать, по форме он гармоничен и красив. До сих пор пытливые умы пытаются разгадать тайну египетского треугольника.
Что такое Египетский треугольник на стройке? В чем его особенность +Фото и Видео
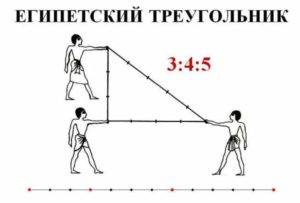Строительство с применением египетского треугольника древний способ, активно используемый до сих пор современными строителями. Название получил благодаря древнеегипетским сооружениям, хотя известно, что история его начинается задолго до этого периода.
Но, скорее всего, свойства уникальной фигуры не были оценены в те времена, пока не появился Пифагор, сумевший проанализировать и оценить изящные формы фигуры.
Египетский треугольник известен еще с древних времен. Он был и остается популярен в строительстве и архитектуре много веков.
Считается, что создал геометрическую конструкцию великий греческий математик Пифагор Самосский. Благодаря ему сегодня мы можем использовать все свойства геометрической постройки в области строения.
Глупая ошибка строителей
«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.
ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет
